Dirac eigenvalues and total scalar curvature
by
Bernd Ammann and Christian Bär
Dirac eigenvalues and total scalar curvature
(.dvi,
.ps,
.ps.gz oder
.pdf)
J. Geom. Phys. 33, 229-234 (2000)
It has recently been conjectured that the eigenvalues
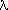 of the
Dirac operator on a closed Riemannian spin manifold M of dimension
n
of the
Dirac operator on a closed Riemannian spin manifold M of dimension
n 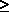 3
can be estimated from below by the total scalar curvature:
3
can be estimated from below by the total scalar curvature:
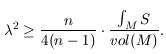
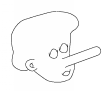
We show by example that such an estimate is impossible. The example
contains a very long and thin cylinder and therefore
looks like a manifold with a very long nose.
 58G25
58G25
Keywords
eigenvalues of the Dirac operator, total scalar curvature, Pinocchio metric
Bernd Ammann, 24.6.1999
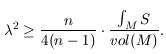
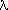 of the
Dirac operator on a closed Riemannian spin manifold M of dimension
n
of the
Dirac operator on a closed Riemannian spin manifold M of dimension
n 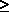 3
can be estimated from below by the total scalar curvature:
3
can be estimated from below by the total scalar curvature: